목적
변형 해석 시 변형이 많이 발생했을 경우 원인 중 하나인 구조적 안정성 여부를 파악하고 싶을 때 이용할 수 있는 좌굴 해석(buckling Analysis)에 대하여 설명 드리겠습니다.
살펴보기
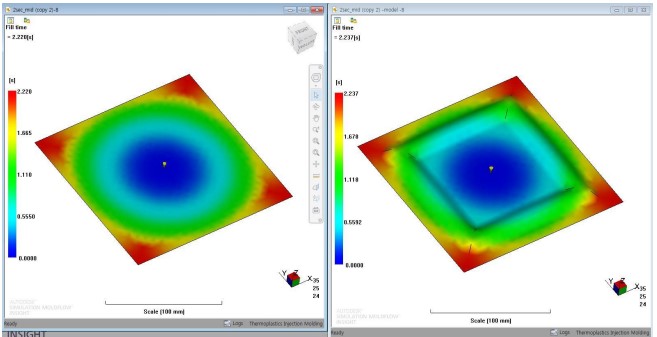
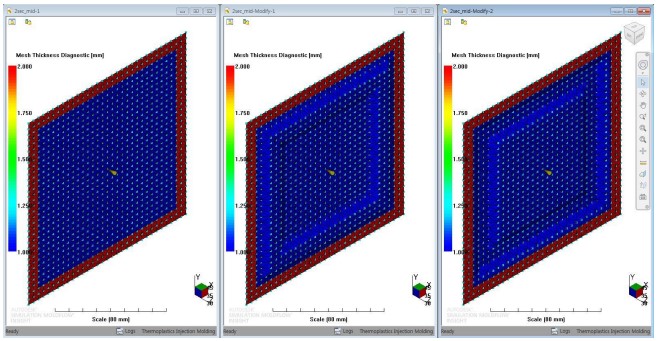
아래 결과는 평판 제품과 가장자리에 돌출 형상이 있는 제품의 충전 해석 결과입니다. 제품의 살두께는 전체적으로 1mm, 테두리는 2mm 인 제품에 미성형 없이 충전 완료 되었습니다.
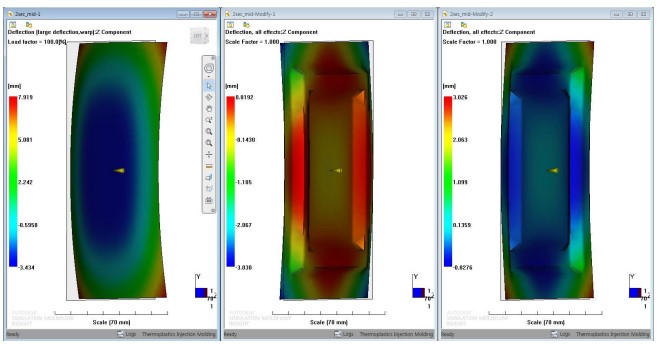
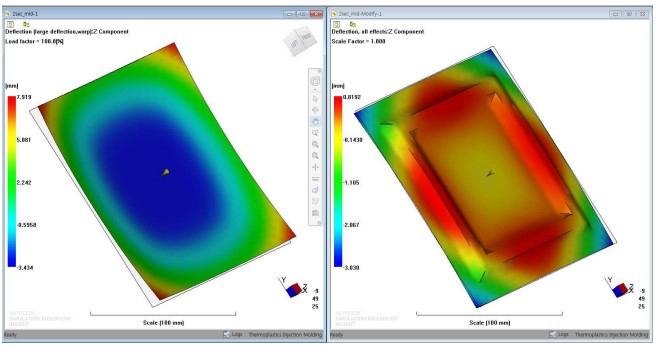
아래와 같이 평판 제품의 변형이 심하게 발생하고 있다. 하지만 굴곡 형상의 변형은 작습니다.
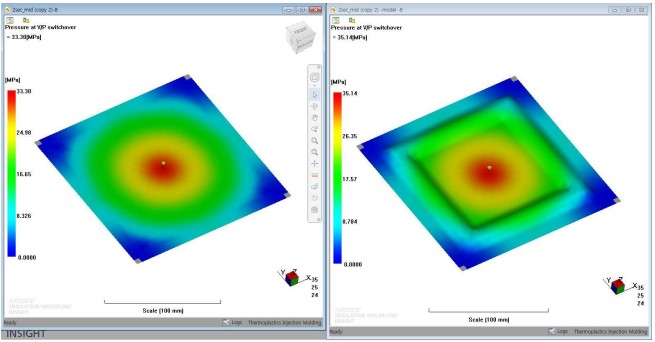
아래와 같이 보압 전환 시점의 압력은 큰 차이가 없습니다.
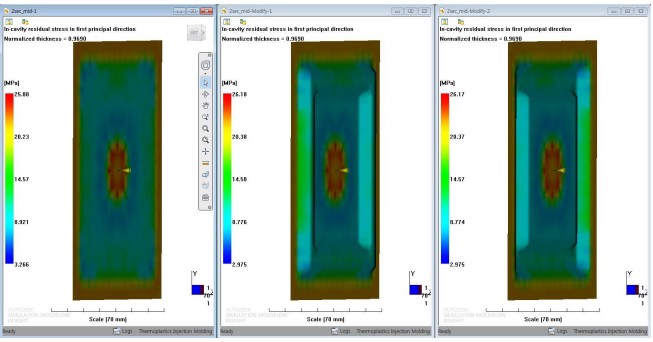
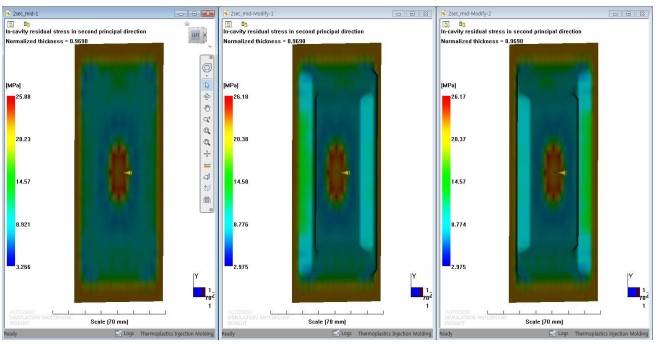
변형을 일으키는 잔류응력은 아래와 같이 두가지 Case 모두 큰 차이 없습니다.
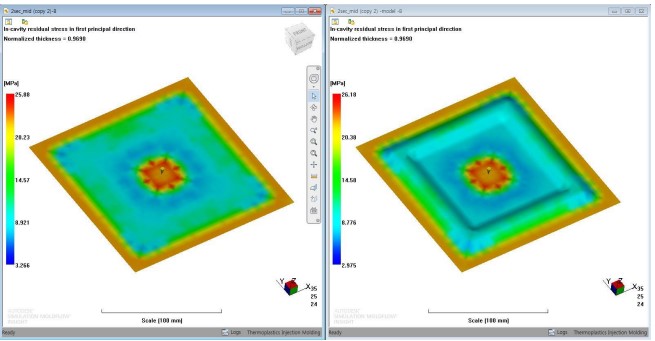
결론적으로 테두리에서 두께가 두껍고 중심에는 두께가 얇기 때문에 수축 편차에 의해 변형이 일어 나지만, 오른쪽 결과의 변형이 작은 이유는 구조적으로 안정된 구조이기 때문인데, 이것을 증명하기가 쉽지 않습니다.
다음 페이지와 같이 좌굴 해석(Buckling)을 선택하여 해석을 수행하세요!
좌굴 해석이란 어느 정도의 응력이 추가적으로 가해져야 제품에 좌굴이 발생할 것인가를 계산하는 것입니다. 좌굴이 발생하는 응력보다 낮은 수축응력이 제품에 가해진다면 선형해석이 가능하며, 그렇지 않다면 비선형 해석으로 변형량을 계산하여야 합니다. 따라서 변형 해석 이전에 좌굴 해석을 선행하여 선형 또는 비선형을 결정하여야 합니다.
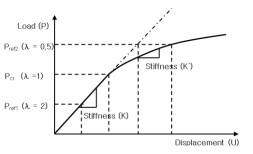
{P}cr λ
cr = {P}ref
{P}cr – 임계응력 (critical force vector)
λcr – Eigenvalue
{P}ref – 참조 응력 (reference force vector)
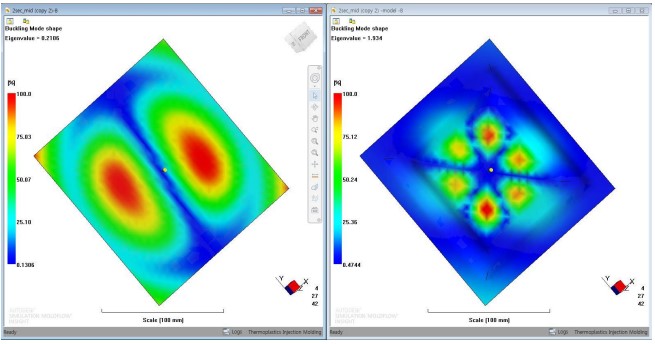
위 그림과 같이 λ(람다)의 값인 Eigenvalue가 1 이하의 경우(Pref2) 하중 대비 변형값이 많이 발생하고, Eigenvalue가 1 이상의 경우(Pref1) 하중 대비 변형 값이 작게 발생합니다. 아래 결과와 같이 판상 제품이 굴곡 제품에 비해 Eigenvalue 가 상당히 작은 것을 확인할 수 있습니다.
아래는 3가지 Case를 상부 굴곡과 하부 굴곡으로 적용했을 때 이용하여 비교한 결과입니다.
제품의 살 두께는 아래와 같습니다.
유동 방향의 변형을 일으키는 잔류응력의 차이는 거의 없습니다.
유동 방향의 직각 방향의 변형을 일으키는 잔류응력의 차이도 거의 없습니다.
아래와 같이 굴곡 형상의 제품의 변형이 평판 형상에 비해 변형량이 개선되는 것을 확인할 수 있습니다.